Алгоритмы

Список вопросов к Python собеседованию

Время выполения алгоритма («О-большое»)

На самом деле, существует не только «большое О», но и ряд других обозначений:

• O(ƒ(n)) – (Big-O) – верхняя граница, «не хуже чем»;
• o(ƒ(n)) – (Little-o) – верхняя граница, «лучше чем»;
• Ω(ƒ(n)) – (Omega) – нижняя граница, «не лучше чем»;
• Θ(ƒ(n)) – (Theta) – точная оценка.

Наиболее часто встречающиеся оценки:

• О(1) - константное время (получение одного элемента в массиве)
• O(log n) - логарифмическое время (бинарный поиск).
• О(n) - линейное время (простой поиск).
• О(n*log n) - линейно-логарифмическое время (эффективные алгоритмы сортировки, напр. быстрая сортировка).
• О(n²) - квадратичное время (медленные алгоритмы сортировки: сортировка выбо­ром).
• О(n³) - кубическое время (Обычное умножение двух n на n матриц).
• О(n!) - очень медленные алгоритмы (задача о коммивояжере полным перебором).

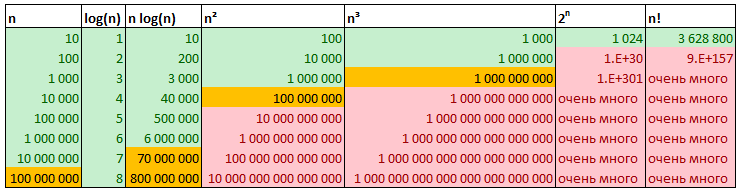
Скорость алгоритмов измеряется не в секундах, а в темпе роста количе­ ства операций.¹

Бинарный поиск

Бинарный поиск - на входе получает отсортированный список элементов. Если искомый элемент присутствует в списке - возвращает его позицию. В противном слу­чае возвращает null.

Time Complexities

• Best case complexity: O(1)
• Average case complexity: O(log n)
• Worst case complexity: O(log n)

The space complexity of the binary search is O(1).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def binary_search(arr: List[int], elem: int) -> Union[int, None]:
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) // 2
        guess = arr[mid]
        if guess == elem:
            return mid
        elif guess > elem:
            high = mid - 1
        else:
            low = mid + 1
    return None

More

Сортировка выбором

Наиболее простая, но медленная сортировка. Сложность О(n²).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

def search_min(arr: List) -> int:
    min_index = 0
    for i in range(len(arr) - 1):
        if arr[min_index] > arr[i]:
            min_index = i
    return min_index


def selection_sort(arr: List) -> List:
    result = []
    copy = arr[:]
    while len(copy) > 0:
        min_index = search_min(copy)
        result.append(copy.pop(min_index))
    return result

More

Рекурсия

Рекурсия - это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ.

Примеры в реальной жизни: эффект Дросте, треугольник Серпинского.

Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде и наоборот.

Рекурсивная функция состоит из:

• Условие остановки / Базовый случай
• Условие продолжения / Шаг рекурсии — способ сведения задачи к более простым.

Рекурсивные функции используют стек вызовов, где каждый вызов создает собственную копию переменной. Обратиться к переменной, принадлежащей другому уровню, невозможно.

Стек — абстрактный тип данных, представляющий собой список элементов, организованных по принципу LIFO (last in — first out).

В Python стеком можно назвать любой список, так как для них доступны операции pop и push.

В интерпретаторе Python (CPython) есть защита от переполнения стека.

Лимит глубины рекурсии можно узнать при помощи функции sys.getrecursionlimit, а изменить этот лимит при помощи sys.setrecursionlimit:

1
2
3
4

import sys
print(sys.getrecursionlimit()) # 997

sys.setrecursionlimit(1500)

Увеличение лимита рекурсии может привести к переполнению стека, поэтому лучше переписать алгоритм итеративно.

Если в гугле ввести слово “рекурсия”, то он наряду с результатми поиска выдаст «возможно, вы имели в виду “рекурсия”» :-)

Быстрая сортировка

Быстродействие быстрой сортировки сильно зависит от выбора опорного элемента.

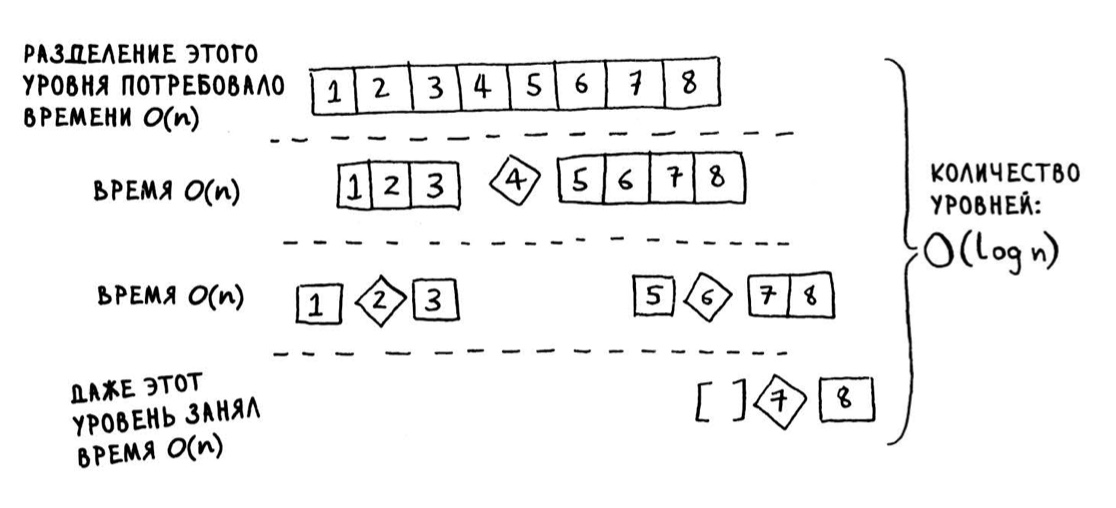
Лучший сценарий: O(n*log n) (он же средний) - когда пограничным элементом выбирается средний, или ближайший к середине.

Худший сценарий: O(n²) - это происходит в случае, если за пограничный элемент берется первый или последний элемент массива.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from typing import List
from random import randint

# top answer on stackoveflow
def quick_sort(arr: List) -> List:
    less = []
    equal = []
    greater = []

    if len(arr) > 1:
        pivot = arr[0]
        # pivot = arr[len(arr) // 2]
        # pivot = randint(0, len(arr) - 1)
        for elem in arr:
            if elem < pivot:
                less.append(elem)
            elif elem == pivot:
                equal.append(elem)
            else:
                greater.append(elem)
        return quick_sort(less) + equal + quick_sort(greater)
    else:
        return arr

# В одну строку =)
def qsort_one_line_mid(arr: List) -> List:
    return (
        arr
        if len(arr) < 2
        else qsort([val for val in arr if val < arr[len(arr) // 2]])
        + [arr[len(arr) // 2]] * arr.count(arr[len(arr) // 2])
        + qsort([val for val in arr if val > arr[len(arr) // 2]])
    )

Существует параллельная версия быстрой сор­ тировки, которая сортирует массив за время О(n).

More

Хеш-таблицы

aka «ассоциативные массивы», «словари», «отображения», «хеш­ карты», «хеши»

В научной терминологии говорят, что хеш-функция «отображает строки на числа».

Хеш-функция должна соответствовать некоторым требованиям:

• Быть последовательной
• Разным строкам должны соответствовать разные числа

Коллизии

Существует много разных стратегий обработки коллизий. Простейшая из них выглядит так: если несколько ключей отображаются на один элемент, в этом элементе создается связанный список.

выбор хеш-функции действительно важен. Хеш-функция, отображаю­ щая все ключи на один элемент массива, никуда не годится. В идеале хеш-функция должна распределять ключи равномерно по всему хешу;

если связанные списки становятся слишком длинными, работа с хеш- таблицей сильно замедляется. Но они не станут слишком длинными при использовании хорошей хеш-функции!

Поиск в ширину (BFS, Breadth-First Search)

BFS - это алгоритм для решения задачи поиска кратчайшего пути.

BFS помогает ответить на вопросы двух типов:

• тип 1: существует ли путь от узла А к узлу В?
• тип 2: как выглядит кратчайший путь от узла А к узлу В (нахо­дит путь с минимальным количеством сегментов)?

Поиск в ширину выполняется за время O(V+E) ( V - количество вершин,Е - количество ребер).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

import collections
def bfs(graph, root):
    visited, queue = set(), collections.deque([root])
    visited.add(root)
    while queue:
        vertex = queue.popleft()
        for neighbour in graph[vertex]:
            if neighbour not in visited:
                visited.add(neighbour)
                queue.append(neighbour)

BFS - это жадный алгоритм.

Алгоритм Дейкстры

Алгоритм Дейкстры - алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.²

Для графов с отрицательными весами - алгоритм Беллмана-Форда.

Ал­горитм Дейкстры работает только с направленными ациклическими графами, которые нередко обозначаются сокращением DAG (Directed Acyclic Graph).

Алгоритм Дейкстры состоит из четырех шагов:

1. Найти узел с наименьшей стоимостью (то есть узел, до которого можно добраться за минимальное время).
2. Проверить, существует ли более дешевый путь к соседям этого узла, и если существует, обновить их стоимости.
3. Повторять, пока это не будет сделано для всех узлов графа.
4. Вычислить итоговый путь.

Алгоритм Дейкстры - это жадный алгоритм.

Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины n рёбрами длины 1, то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.

Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут.

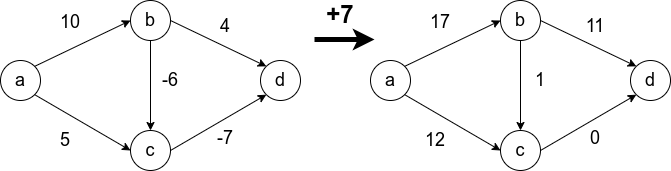
В оригинале путь проходит через a -> b -> c -> d, а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через a -> c -> d.

Эффективная реализация предполагает использование кучи.

Статья с кодом

Статья на Хабре

Жадные алгоритмы

Жадный алгоритм прост: на каж­дом шаге он выбирает оптимальный вариант. В техни­ческой терминологии: на каждом шаге выбирается локально-оптимальное решение, а в итоге мы получаем глобально-оптимальное решение.

Иногда идеальное - враг хорошего. В некоторых случаях достаточно алгоритма, способного решить задачу достаточно хорошо. И в таких областях жадные алгоритмы работают просто отлично, потому что они просто реализуются, а получен­ное решение обычно близко к оптимуму.

Когда вычисление точного реше­ния занимает слишком много времени, применяется приближенный алго­ритм. Эффективность приближенного алгоритма оценивается по быстроте и близости полученного решения к оптимальному.

NP-полные задачи

Задача о коммивояжере и задача покрытия множества

Не существует простого способа определить, является ли задача, с которой вы работаете, NР-полной. Несколько характерных признаков:

• алгоритм быстро работает при малом количестве элементов, но сильно замедляется при увеличении их числа;
• формулировка «все комбинации х» часто указывает на NР-полноту за­дачи;
• приходится вычислять все возможные варианты Х, потому что за­дачу невозможно разбить на меньшие подзадачи? Такая задача может оказаться NР-полной;
• если в задаче встречается некоторая последовательность (например, последовательность городов, как в задаче о коммивояжере) и задача не имеет простого решения, она может оказаться NР-полной;
• если в задаче встречается некоторое множество и задача не имеет простого решения, она может оказаться NР-полной;
• можно ли переформулировать задачу в условиях задачи покрытия множества или задачи о коммивояжере? В таком случае задача определенно является NР-полной.

У NР-полных задач не существует известных быстрых решений.

Динамическое программирование

• Динамическое программирование применяется при оптимизации не­ которой характеристики.
• Динамическое программирование работает только в ситуациях, в кото­рых задача может быть разбита на автономные подзадачи.
• В каждом решении из области динамического программирования стро­ится таблица.
• Значения ячеек таблицы обычно соответствуют оптимизируемой харак­теристике.
• Каждая ячейка представляет подзадачу, поэтому нужно думать о том, как разбить задачу на подзадачи.
• Не существует единой формулы для вычисления решений методом ди­намического программирования.

Расстояние Левенштейна оцени­вает, насколько похожи две строки , а для его вычисления применяется динамическое программирование.

Алгоритм Фейнмана

Алгоритм Фейнмана, названный по имени известного физика Ричарда Фейнмана, работает так:

1. Записать формулировку задачи.
2. Хорошенько подумать.
3. Записать решение.

Алгоритм k ближайших соседей

Алгоритм k ближайших соседей применяется для классификации и ре­грессии. В нем используется проверка k ближайших соседей.

• Классификация = распределение по категориям.
• Регрессия = прогнозирование результата.
• «Извлечением признаков» называется преобразование элемента в список чисел, которые могут ис­пользоваться для сравнения.
• Качественный выбор признаков - важная часть успешного алгоритма k ближайших соседей.

Преобразование Фурье

Фильтры Блума и Hyperloglog

Параллельные алгоритмы

Распределенные алгоритмы

Алгоритмы SHA

Алгоритм Диффи-Хеллмана

Линейное программирование

DFS

Направленный / ненаправленный граф Взвешенный / невзвешенный граф Дерево в-деревья; красно-черные деревья; кучи; скошенные (splay) деревья.